This view, I believe, represents the mainstream contemporary beliefs of most people who theorize about research methodology. It fully accepts the increasingly common view among scholars in the 20th century that anything simple must be guided by ideology rather than by a "true" understanding of reality, by "careful" consideration of alternative viewpoints, or by a "diligent" attention to complexities. The implication is that those who propose simple theories are themselves simple-minded, and most likely motivated by something other than research, for example by religious beliefs or wishful thinking.
There are, of course, people on the other side of this debate: people who believe that there are simple, unitary, and strikingly clear explanations for reality, and that those who insist on convoluted theories are simply caught up in their own academic gobbledygook and a refusal to acknowledge what they know in their hearts (if only they'd listen to them) to be true.
(Need I make explicit allusion here to one example of how this debate plays out; namely, between the policy makers in the current administration who insist that all educational programs be supported by double-blind controlled experiments--i.e. by simple data and analysis--and those post-modernist theorists and methodologists who insist that much of reality cannot possibly be understood using such simple methods? Well, I will make such an allusion anyway!)
While--as a tweedy intellectual academic myself--I usually side with the post-modernist people who seek complexity and convolution, one comment of Aaron's caught my attention. He wrote:
(One key limitation of this picture is the straightness of the different axes. In actuality, as one moves out along the axis of “texture,” for example, one necessarily moves closer to both other axes, since teasing out complexities will increasingly require reference to the writings of others and to unexplained aspects of the context under examination. Thus, imagine that all of these axes curve towards each other (which I don’t know how to do in my simple drawing program.)
I have spent the last few days thinking about what this schematic would look like if the axes curved toward one another as Aaron describes. It's difficult to visualize (mainly becuase there are THREE axes--hence a three-dimensional space: hard to visuallize, let alone draw. But one thing is clear: if the axes curve toward one another, then eventually, at some point "out there," they would intersect.
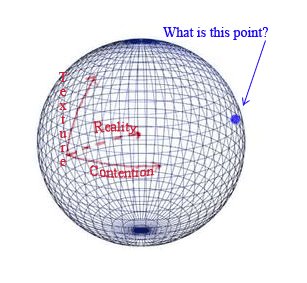 Because I can't draw anything truly three-dimensional, I've chosen to "sort of" represent what this would look like with curved axes. I've drawn two of the axes on the surface of a sphere, with the third axis sort of tending toward the center of the sphere. Then, I've imagined that the three axes eventually intersect at some point on the other side of the sphere. Thus:
Because I can't draw anything truly three-dimensional, I've chosen to "sort of" represent what this would look like with curved axes. I've drawn two of the axes on the surface of a sphere, with the third axis sort of tending toward the center of the sphere. Then, I've imagined that the three axes eventually intersect at some point on the other side of the sphere. Thus:What this leads me to imagine is, What the heck is that point of intersection on the other side? Is it, perhaps, the point-of-view of someone who holds that the best theory is one in which texture, contention, and reality finally come together into a grand theory that supercedes all of the silly vain attempts of intellectuals to strive toward more and more complexity, that is, the unified field theory (if you will) that embraces unity, simplicity, and universality?
What if Aaron's notions of sophistication are only half the story, that once a theory has incorporated all that complexity and contention and convolution that eventually it evolves into something truly elegant? Maybe "sophistication" cannot be measured purely by complexity? Or, maybe what Aaron is really saying is that he wants his STUDENTS to embrace complexity so that they eventually learn to listen to their hearts?
Occam's Razor, anyone?

2 comments:
"And every year I conclude what William of Occam (that first, great modern William, a William for his time and ours, all the William we will ever need, who gave to us his magnificent razor by which to gauge simple truth, who was exiled and relinquished his life that our academic sins might be forgiven) would have concluded - that there will be no faculty purge this year...What there will probably be next year is more belt tightening, more denied sabbaticals, an extension of the hiring freeze, a reduced photocopy budget. What there will certainly be next year is another April, and another round of rumors." -from _Straight Man_ by Richard Russo (1997)
What a wonderful post, Craig! Can I say “elegant”?
Some thoughts
1. In terms of the point where all the axes converge, it is important to keep Gouldner’s point in mind: that “clarity is always dependent not on good but on poor vision.” The point of intersection, where all of the possible complexity is captured, then, would also be a point of total incoherence, where the capacity to theorize completely breaks down. It may be that the graph should have the axes come together more like the tails of a normal curve, where they come closer and closer but never meet. There is something like a “golden mean” argument within Gouldner’s quote—that only a balance of complexity and clarity allows theory to actually illuminate a phenomenon under consideration. (How you would graph this, I don’t know.)
2. If the intersection point is where theory completely breaks down, it would seem to be a place that could only be inhabited by God, or by a Buddha. I say a Buddha, because high level buddhist practitioners, it is said, don’t actually”think” the way you or I do. Of course, they can “think” if they want to, but they generally exist in a complete and integrated engagement with their environment. Thus, when you ask a Tibetan Llama “why” he or she has decided on a particular course of action, she may answer “why do you always ask why?” They act in response to what they sense the situation demands, not in response to abstract arguments. The argument (which I think is more than debatable) is that this state of integration is a state of enlightenment, in which the best possible option is more likely to be chosen. (Interestingly, they are said not to have “memories” either. They live almost completely in the present, and the importance of the past increasingly emerges only as a presently embodied historically acquired adjustment to the world—this takes Dewey’s argument that history is most important in the present to the extreme).
3. I’m not sure what to say about the relationship between complexity and elegance, although it seems crucial. Again, the importance of an elegant theory may be that it illuminates some aspect of the world in sharp relief. Think of E=MC^2. It elegantly describes a relationship between matter and energy, but does not attempt to capture everything about this relationship, as quantum physics (which doesn’t seem very elegant to me, but maybe because I don’t understand it) shows. I think what this implies is not that everyone become postmodern convolutionists in their writing, as Craig points out, but that scholars understand some of the limits of their theories even as they (may) seek to present them in an elegant form. In my own work, I have tried to do this, in part, by ending with a discussion of some of the ways a particular theory I have been describing seems to fail, without destroying what I hope is the at least slightly elegant argument I have made.
4. Taking Craig’s “elegance” point seriously also implies that there may be cases where a scholar whose theoretical understandings fall very close to the vertex, e.g., taking on an extremely simple form in multiple ways, actually turns out to be extremely useful and “elegant” for others. Which also helps point at the limits, again, of my own theorizing around this issue.
Of course, this could also be framed as a “theory/practice” issue, in that any abstract theory always must be appropriated (made tacit and not theoretical) if it is to be of use in a particular context. Bourdieu, for example, writes that the concepts he developed
“were intended, among other things, to point out that there is a practical knowledgte that has its own logic, which cannot be reduced to that of theoretical knowledge; that in a sense, agents know the social world better than theoreticians” (cited in Reay, 2004, p. 438).
As usual, I seem unable to respond succinctly. . . .
I want to note that we seem to have naturally come to what seems (to me) like a good balance between “posts” and “comments.” Craig’s contribution seems worthy of “posting” on the front page, while the contributions of the rest of us have seemed more like comments.
Reay, D. (2004). “It’s all becoming a habitus”: Beyond the habitual use of habitus in educational research. British Journal of Sociology of Education, 25(4), 431-444.
Post a Comment